【注意】本文粗体字母为矢量。
磁场看不见摸不着,又实实在在的存在着,它的本质到底是什么,往往给人有很神秘的感觉。现在主流科学界认为磁场是一种特殊的物质。
相对论认为,一个电荷相对于某一个观察者运动, 在这个观察者看来,该电荷在周围空间除产生电场外,还产生磁场,但在另外一个随电荷一同运动的观察者看来,这电荷是静止的,它周围就不存在磁场了。磁场既然是一种物质,怎么可能在一个人看来是有的,在另一个人看来是没有的?
大家想一想,自然界中有什么物质在一个人看来是有的,在另一个人看来是没有的?
有一个物体存在于空间中某个地方,一个人说它是真实存在的,一个人说它是不存在的,而且两人的说法都是正确的,这怎么可能呢?
很多人马上就说相对论是错误的,事情没有那么的简单。如果我们假定相对论是正确的,我们抓住了这种认识上的矛盾性,实际上就可以给磁场的本质做出判断。
我认为我们不应该把电磁场的本质看作是一种特殊物质,场的本质是物质相对于我们观察者运动所表现出的一种性质而不是物质本身。
举例来讲:我们眼前的一棵树、一条河是“物”,树的生长、河水的流动是“事”,这就是我们常说的事物。
物质就像一棵树、一条河,是“物”,场就像树的生长、河水的流动是“事"。
场的本质就是物质相对于我们观察者运动变化的一种表现,你把场看成是一种特殊的物质,这就是“事”和“物”不分的思想。
把场的本质看成是“事”,就像是上面所说的河水的流动,我们就很容易理解磁场相对于一个人是存在的,相对于另一个人是不存在的。
我们说一条河相对于一个人是存在的,相对于另一个人是不存在的,这肯定是荒唐的。
我们说河水的流动相对于一个人是存在的,相对于另一个人(随水流动的人)是不存在的,这肯定是有可能的。
认定场的本质就是物质相对于我们观察者运动变化的一种表现,那是什么物质在运动?
我的回答是空间!
我们只要假定:宇宙中任何一个相对于我们观察者静止的物质点周围空间都是以光速辐射式的运动,就可以解释电磁场的一切规律。
我们习惯了描述物体在空间中的运动,那我们又如何定性定量的描述空间本身的运动?
一条直线,我们可以看则是由无数个点构成,一个平面我们也可以看则是由无数个点构成,同样道理,我们可以把三维空间看则是由许多个点构成,称之为空间几何点,描述这些几何点的运动,就可以描述出空间的运动。
下面,我们来结合数学中场的定义来给出电磁场本质正确、精确的解释。
在数学中场的定义为:若空间中(或空间的某一部分),每一个点对应一个确定的量,则称这样的空间为场,当空间中每一点所对应的量为数量时,则该空间为数量场,当空间中每一个点所对应的量是一个矢量时,则称这样的空间为矢量场。
从数学中场的定义可知,场是用空间的点函数来表示的,反之,若给出空间中某一个点函数,就给出了一个场。
把场看成是运动的空间,结合数学中场的定义,我们给物理中重力场、电磁场、核力场下一个统一的定义:
相对于我们观察者,物质点周围空间中任意一个空间几何点指向该物质点的位移矢量随空间位置变化或者随时间变化,这样的空间称为物理场,也可以叫物理力场。
简单一句话,物理三大场本质就是运动变化的空间,从以上的定义可以知道,物理三大场都是矢量场。
首先我们用运动空间来定义电荷、电场:
设想一个物质点O相对于我们观测者静止,在某一个时刻,任意一个几何点P从O点出发,以光速度C【光速某些情况下可以看成矢量,用粗字体C表示矢量光速度,而标量光速用细字体C表示】沿某一个方向直线运动,射向周围无限远处空间。
从O点指向P点的矢径为R。让点O处于直角坐标系xyz的原点,矢径R是xyz和时间t的函数,随xyz的变化又随t的变化而变化,记为R = R(x,y,z,t)。
在我们观测者看来,物质点O具有正电量q是指周围有N条几何点的光速度C射向无限远处空间【负电荷是几何点从无限远处空间汇聚到电荷上的】,并且光速度C呈辐射状均匀分布。在O点周围以R的长度为半径作一个高斯包围面S,把S分割成N块,每一块面元ds上有dn条光速度C垂直穿过去。
E = k dn C/ds
上式中E就是正电场,K为比例常数。E的方向和光速度C方向一致。
也可以用把高斯面S无限分割成许多矢量面元ds【我们规定指向S内侧为负,外侧为正】,用ds的方向来表示E的方向。
E = k dn C【s】/ds
【s】为沿ds方向的单位矢量。
如果把n取1,式E = k dn C/ds
可以为:E = k C/△S【E】或者E = k C/△S
【E】为沿E方向的单位矢量。△S为高斯面S其中的一小块。
式E = k C/△S【E】或者E = k C/△S可以称为电场的几何定义方程。
如果用【c】表示C的单位矢量,上也可以写成:
E = k C【c】/△S
由式E = k dn C/ds可以导出式E·ds =k C dn
对式E·ds = k C dn两边积分,结果为k’q=∮E·ds= k C N
K’为比例常数,∮为包围O点封闭曲面积分,q就是正电荷的电量,电荷的电量几何意义就是O点周围有N条几何点的光速C。
我们接着来给磁场下一个几何定义。
以上的点电荷O,相对于我们观察者静止,在周围空间P处产生了静电场E,当O点相对于我们观察者以速度v运动的时候,在O点周围空间P处还产生了磁场B。
我们的大致思路是:O点相对于我们静止时候,周围空间以光速辐射式的运动,我们用一个高斯面S包围O点,S上一小块面积△S垂直穿过几何点的光速度C的条数反映了这个地方的电场强度E,也就是E =k C/△S。
当O点相对于我们以速度v运动,会引起v垂直方向的电场的变化,磁场的本质就是电场变化的那部分。
从实验发现,磁场B的方向和电场E方向、电荷运动速度v方向相互垂直时候,磁场最强,可以判断,B,E,v满足于叉乘关系。
B = a’(v ×E)
a’为常数,由于光速度C和E平行,因而式B = a’(v ×E)可以写为:B = a(v ×C).
接下来我们来确定常数a的值。
B的数量应该取决于速度v和光速度C 数量的比值,还有,B描述的是空间局部性质,因而和电场一样是空间位置函数,随空间位置【这里是矢量面元ds或者高斯面S其中一小块面积△S】而变化。
可以说,B的数量应该为:B = 常数(v /C △S)
B的方向由式B = a(v×C)决定。综合两式,可以得出:
B = 常数(v ×C)/ C 2△S
或者B = 常数(v ×【c】)/ C △S
这个就是磁场B 的几何定义方程。注意,以上的沿v垂直平面内分布许多条的光速度C,这样还产生沿v垂直方向许多条B,呈环绕状。所以,磁场是环绕形状的。
利用以上的电场几何定义式E = k C/△S和磁场几何定义式B = 常数(v ×C)/ C2△S
很容易导出磁场B是电场E的相对论性效应:
B = v × E/ C2
上个月在网上买了三本相对论教材和一本《量子力学概论》,本打算好好研究下相对论的数学体系,可是书到了之后,我却深深地被量子力学吸引住了,不停在研读。而且在研究量子力学的同时,我的线性代数和微分方程知识也增加了不少,这确实是我没有想到的。在我看来,不管是狭义相对论还是广义相对论,它本质上都是一种几何理论,你总要想象从一个参考系观测会发生什么,然后从另外一个参考系又会看到什么;而量子力学虽然对我来讲一切都是新鲜的,但是它的数学性比较强,主要是微分方程的求解和理解。我想这也是我对量子力学更感兴趣的原因吧,因为我善于代数而不善于几何。
量子力学中让我最神往的内容莫过于费曼所发明的路径积分形式。资料记载费曼用他发明的方法在一个晚上就算出了别人几个月才算出来的结果,可见路径积分形式的优越性。当然,我也清楚,这个路径积分并不简单,它涉及到了泛函积分这一非常高深的内容,对于我这个连数学分析都还没有学好的小孩来说,泛函是难以触摸的。不过,我还是尽量想办法向它靠近。为此,我还浏览到了一些不少让人兴奋的内容,比如薛定谔的方程的推导、力学-光学类比、雅可比方程等等。
很遗憾,在正统的量子力学教材中,这些让我很兴奋的内容却鲜有涉及,有的话大多数都是一笔带过的感觉。多数量子力学不会讲到路径积分,就算有也只是作为附录。对于薛定谔方程的推导,也没有涉及到。这也让我养成了一个习惯意识:书本最有趣的东西往往都是在附录。所以对于教科书,那么写得正正式式的内容我一概没有兴趣,那些附录内容才是我最喜欢读的。可是,那些让人兴奋的内容却不一定是很难的,就像下面的薛定谔方程的启发式推导,它不仅不难,而且易于理解。
===薛定谔方程===
在量子力学诞生之前,科学家已经通过实验发现光既有波动性也有粒子性,而德布罗意提出也同时具有波动性和粒子性,这些都奠定了量子力学的基础。根据量子论,一个光子的能量可以由










,其中














。
同时,光子也具有动量,其大小为






,其中




。这些性质在波和粒子之间是可以通用的,因为它们的波粒二象性。
对于最简单的一维简谐波,我们可以将它的方程写成












。我们可以这样理解它,在















































,可见其实数部分就是一维简谐波的方程。
由于实物粒子具有波动性,那么我们就应该给粒子一个波动方程,我们以最简单的简谐波形式来考虑,即
















。下面的过程是显然的:


































类比经典力学的,考虑保守系统,有“能量=动能+势能”,即




















。所以上式变成:


















其中:




















代入就得到:





















这就是薛定谔方程,是一道线性偏微分方程。
有些敏感的读者会发现,从







可以直接得到













,然后代入就得到:
























难道这一道也是薛定谔方程的等价形式?
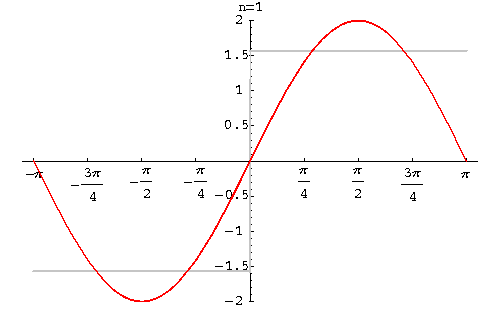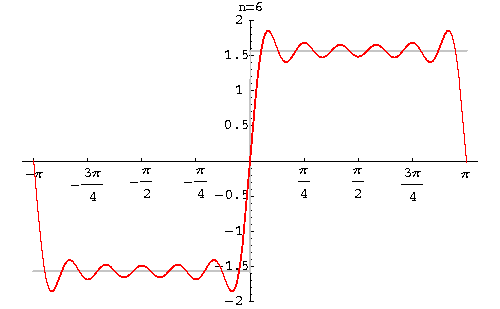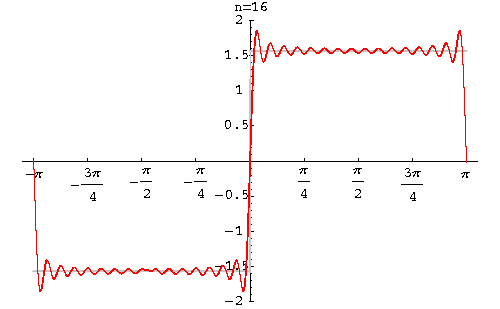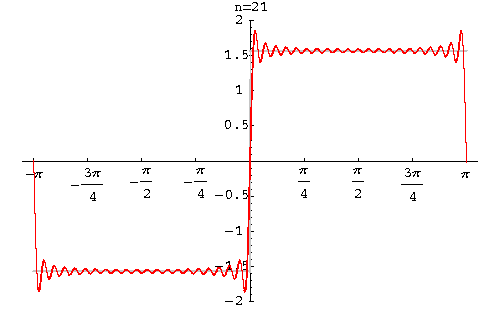
当然不是,由于我们上面的是“启发式引导”,因此我们考虑的是最简单的简谐波,所以才得到不同的形式。不过由傅里叶级数的知识可以知道,再复杂的波也可以用频率不同的简谐波叠加而成,因此我们得到的方程必须满足“两个解叠加之后还是原方程的解”,也就是说,只有线性形式的薛定谔方程





















才是正确的量子力学波动方程。说白了,就是说波动方程必须是线性的。
===总结一下===
很明显,上面只是一种形式和数学的处理,我们还没有赋予它物理意义,比如波函数的具体意义等都还没有给出,而且结果的正确性还有待检验。这并不属于严格推导,所以我强调是启发性的思考。但是量子力学教程告诉我们,这是正确的。对于量子力学入门来说,这也足够了。读者也应该清楚,这个过程并不难,甚至有点出乎意料的简单了。不过我还没有发现哪本量子力学教材提到过,它们都去缺乏这些创意性的、启发性的思考,而充满了复杂的分析计算。也许是我读的书太少了吧。又或者是每个人的学习思路都不同吧,我只是觉得,虽然不是每个人都可以学好量子力学,但每个人都可以学一些量子力学的。
Jack
Fedora 发行计时器
搜索
最新评论
日历
| 二月 | ||||||
|---|---|---|---|---|---|---|
| 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 26 | 27 | 28 | 29 | 30 | 31 | 1 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 1 |